k-means for Customer Segmentation

Customer segmentation is the practice of partitioning a customer base into groups of individuals that have similar characteristics
machine learning
Published

February 9, 2022

Imagine that you have a customer dataset, and you are interested in exploring the behavior of your customers using their historical data.
Customer segmentation is the practice of partitioning a customer base into groups of individuals that have similar characteristics. It is a significant strategy as a business can target these specific groups of customers and effectively allocate marketing resources.

The dataset being worked on consists of 850 customers, with information about their income and debt. You can download the data set here: https://cocl.us/customer_dataset

import random # library for random number generation
import numpy as np # library for vectorized computation
import pandas as pd # library to process data as dataframes

import matplotlib.pyplot as plt # plotting library
# backend for rendering plots within the browser
%matplotlib inline 

from sklearn.cluster import KMeans 
from sklearn.datasets.samples_generator import make_blobs

print('Libraries imported.')
Libraries imported.

Read the data into a pandas dataframe.

customers_df = pd.read_csv('Cust_Segmentation.csv')
customers_df.head()
Customer Id Age Edu Years Employed Income Card Debt Other Debt Defaulted Address DebtIncomeRatio
0 1 41 2 6 19 0.124 1.073 0.0 NBA001 6.3
1 2 47 1 26 100 4.582 8.218 0.0 NBA021 12.8
2 3 33 2 10 57 6.111 5.802 1.0 NBA013 20.9
3 4 29 2 4 19 0.681 0.516 0.0 NBA009 6.3
4 5 47 1 31 253 9.308 8.908 0.0 NBA008 7.2

Preprocessing the data

Address in this dataset is a categorical variable. k-means algorithm isn’t directly applicable to categorical variables because the Euclidean distance function isn’t really meaningful for discrete variables.
So let’s drop this feature and run clustering.

df = customers_df.drop('Address', axis=1)
df.head()
Customer Id Age Edu Years Employed Income Card Debt Other Debt Defaulted DebtIncomeRatio
0 1 41 2 6 19 0.124 1.073 0.0 6.3
1 2 47 1 26 100 4.582 8.218 0.0 12.8
2 3 33 2 10 57 6.111 5.802 1.0 20.9
3 4 29 2 4 19 0.681 0.516 0.0 6.3
4 5 47 1 31 253 9.308 8.908 0.0 7.2

Normalize the dataset using StandardScalar(). Normalization is a statistical method that helps mathematical-based algorithms interpret features with different magnitudes and distributions equally.

from sklearn.preprocessing import StandardScaler

X = df.values[:,1:]
X = np.nan_to_num(X)
cluster_dataset = StandardScaler().fit_transform(X)
cluster_dataset
array([[ 0.74291541,  0.31212243, -0.37878978, ..., -0.59048916,
        -0.52379654, -0.57652509],
       [ 1.48949049, -0.76634938,  2.5737211 , ...,  1.51296181,
        -0.52379654,  0.39138677],
       [-0.25251804,  0.31212243,  0.2117124 , ...,  0.80170393,
         1.90913822,  1.59755385],
       ...,
       [-1.24795149,  2.46906604, -1.26454304, ...,  0.03863257,
         1.90913822,  3.45892281],
       [-0.37694723, -0.76634938,  0.50696349, ..., -0.70147601,
        -0.52379654, -1.08281745],
       [ 2.1116364 , -0.76634938,  1.09746566, ...,  0.16463355,
        -0.52379654, -0.2340332 ]])

Modeling

Let’s run our model and group the customers into three clusters.

num_clusters = 3

k_means = KMeans(init='k-means++', n_clusters=num_clusters, n_init=12)
k_means.fit(cluster_dataset)
labels = k_means.labels_
print(labels)
[1 2 0 1 2 2 1 1 1 2 0 1 1 1 0 1 1 1 2 1 1 1 0 2 2 1 1 1 1 1 1 2 0 1 1 1 0
 0 1 2 0 2 1 2 1 2 1 1 1 1 2 2 0 1 0 0 0 1 1 1 2 1 2 2 1 1 1 0 1 0 1 1 1 1
 1 1 1 1 2 1 1 0 2 1 2 1 1 1 0 0 1 1 0 0 1 1 1 1 0 1 0 2 1 0 0 2 1 1 1 1 1
 1 1 0 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 2 1 1 0
 1 1 1 2 0 1 1 1 1 2 0 0 1 2 1 1 1 1 1 1 1 1 2 1 1 0 1 0 1 1 0 2 0 1 1 2 0
 2 1 1 1 1 1 2 1 0 1 1 1 2 2 1 2 1 0 1 1 0 1 2 1 0 1 1 1 1 1 0 0 2 1 1 0 2
 1 1 1 1 2 1 1 0 1 1 1 1 2 1 1 0 2 1 1 1 1 1 1 2 1 2 1 1 1 1 1 1 2 0 1 0 1
 1 1 2 1 0 2 0 1 2 1 1 0 1 1 1 1 0 0 0 1 1 1 2 1 1 2 1 2 1 1 2 1 1 1 0 1 1
 0 1 0 2 1 1 1 1 0 1 1 0 0 1 1 1 1 1 1 1 1 0 1 0 2 1 0 1 1 1 0 0 1 1 1 2 0
 1 1 0 1 2 1 1 1 1 1 0 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 2 0 1 0 1 1 1 2 2 1
 0 1 2 0 0 1 1 1 0 1 1 1 1 1 2 1 2 1 1 1 1 0 1 0 1 1 1 2 1 1 1 1 0 1 1 0 0
 2 1 1 1 1 1 0 0 1 2 0 2 1 1 0 1 1 2 2 1 0 1 1 2 1 0 1 2 1 1 1 2 1 1 1 1 2
 1 0 1 1 1 1 2 0 1 1 2 1 0 1 1 2 1 2 1 1 1 1 1 1 1 2 2 1 1 2 1 0 1 1 1 0 1
 0 1 1 1 1 1 2 0 0 1 2 1 2 1 1 0 2 1 0 0 0 2 2 0 1 1 0 1 0 0 1 0 2 1 1 0 1
 0 2 0 1 1 0 1 1 0 0 0 1 1 1 2 2 1 1 0 1 1 0 2 1 0 1 1 1 0 1 2 1 2 2 1 2 1
 1 2 1 0 1 1 1 1 0 0 1 2 1 2 1 1 2 1 0 1 0 1 0 0 0 2 0 1 1 1 0 1 1 1 2 1 2
 1 0 0 1 1 1 1 1 1 1 0 2 1 2 1 1 0 1 1 1 0 1 1 0 0 0 0 1 2 1 0 0 1 1 1 1 2
 2 1 0 1 1 2 1 1 2 1 2 1 1 2 0 2 2 2 0 1 1 0 1 2 2 1 1 1 2 0 1 1 1 1 2 1 1
 1 1 1 0 1 1 2 1 1 2 1 1 1 1 1 1 0 2 1 1 0 1 1 1 1 0 1 2 1 1 2 1 1 0 1 0 1
 0 0 1 1 1 2 0 2 1 2 2 1 0 1 2 1 2 1 1 1 1 1 2 1 0 1 1 2 2 1 1 2 1 1 1 1 1
 1 1 1 0 1 1 2 1 1 1 1 1 1 1 0 1 1 1 2 0 2 2 1 1 1 0 1 1 1 0 0 1 0 1 1 1 2
 1 1 1 1 1 1 1 2 1 1 1 1 1 1 2 2 0 0 1 0 1 1 1 1 2 0 1 1 1 1 1 2 0 1 1 1 0
 1 1 0 1 1 1 1 1 1 0 0 2 2 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 2]

Insights

Each row in the dataset represents a customer, and therefore, each row is assigned a label.

df['Labels'] = labels
df.head()
Customer Id Age Edu Years Employed Income Card Debt Other Debt Defaulted DebtIncomeRatio Labels
0 1 41 2 6 19 0.124 1.073 0.0 6.3 1
1 2 47 1 26 100 4.582 8.218 0.0 12.8 2
2 3 33 2 10 57 6.111 5.802 1.0 20.9 0
3 4 29 2 4 19 0.681 0.516 0.0 6.3 1
4 5 47 1 31 253 9.308 8.908 0.0 7.2 2

Check the centroid values by averaging the features in each cluster.

df.groupby('Labels').mean()
Customer Id Age Edu Years Employed Income Card Debt Other Debt Defaulted DebtIncomeRatio
Labels
0 424.451807 31.891566 1.861446 3.963855 31.789157 1.576675 2.843355 0.993939 13.994578
1 426.122905 33.817505 1.603352 7.625698 36.143389 0.853128 1.816855 0.000000 7.964991
2 424.408163 43.000000 1.931973 17.197279 101.959184 4.220673 7.954483 0.162393 13.915646

Let’s look at the distribution of customers based on their age and income.

area = np.pi * ( X[:, 1])**2  
plt.scatter(X[:, 0], X[:, 3], s=area, c=labels.astype(np.float), alpha=0.5)
plt.xlabel('Age', fontsize=16)
plt.ylabel('Income', fontsize=16)
plt.show()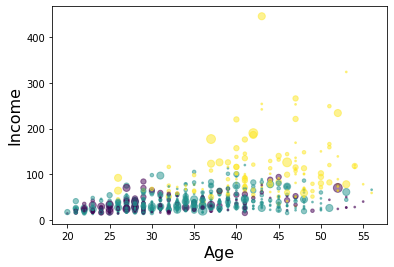

from mpl_toolkits.mplot3d import Axes3D 
fig = plt.figure(1, figsize=(8, 6))
plt.clf()
ax = Axes3D(fig, rect=[0, 0, .95, 1], elev=48, azim=134)

plt.cla()
ax.set_xlabel('Age')
ax.set_ylabel('Income')
ax.set_zlabel('DebtIncomeRatio')

ax.scatter(X[:, 1], X[:, 0], X[:, 3], c= labels.astype(np.float))
<mpl_toolkits.mplot3d.art3d.Path3DCollection at 0x1a21784a90>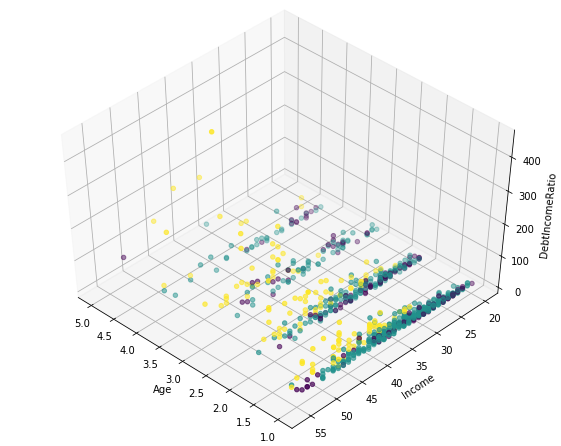

k-means will partition the customers into three groups since we specified the algorithm to generate three clusters. The customers in each cluster are similar to each other in terms of the features included in the dataset.
We can create a profile for each group, considering the common characteristics of each cluster. For example, the three clusters can be: - older, high income, and indebted - middle-aged, middle income, and financially responsible - young, low income, and indebted

You can devise your own profiles based on the means above and come up with labels that you think best describe each cluster.